做 datalab 的心路历程总结

1. bitXor 函数

只用 ~ 和 & 实现x ^ y实现异或，我的思路是:

x y x^y
101 100 001
1 1 0
0 0 0
1 0 1
  1. &后为 1，那么两个数该位都是 1
  2. 我需要找&后为 0，并且该位只有一个 0(todo)
  3. &后为 0，并且两个数该位都是 0
  • 所以 a & b = c 位为 1 的就找到上面的 1.
  • ~a & ~b = d 位为 1 的就找到上面的 3.
  • ~c & ~d推出上面的 2.

2. tmin 函数

返回补码表示的最小整数

  • 直接最高位为 1, 其余全 0 即可
  • 也就是-2^31 + ...最小, 所以…全取 0

3. isTmax 函数

返回是否为补码表示的最大整数

  • x 如果是 Tmax,有~(x+1) ^ x这个是 0,再取个!
  • but x = -1,这个也满足,需要特判,加上& !!(x+1)

4. allOddBits 函数

若奇数位上全为 1 返回 1,否则 0

原始思路每 8 位检查一下(op 次数超了):

1
2
3
4
5
int allOddBits(int x) {
  int mask = 0xaa;
  return !((x & mask) ^ mask) & !((x >> 8 & mask) ^ mask) &
         !((x >> 16 & mask) ^ mask) & !((x >> 24 & mask) ^ mask);
}

改进思路构造出0xaaaa_aaaa这个掩码(9 次):

1
2
3
4
5
int allOddBits(int x) {
  int mask = 0xaa;
  mask = (mask << 24) | ((mask << 16) | ((mask << 8) | mask));
  return !((x & mask) ^ mask);
}

进一步小改进(7 次)

1
2
3
4
5
6
int allOddBits(int x) {
  int mask = 0xaa;
  mask = ((mask << 8) | mask); // 构造出0xaaaa
  mask = (mask << 16) | mask;
  return !((x & mask) ^ mask);
}

笔记: a == b 等价于 !(a ^ b)

5. negate 函数

返回-x(32bit 补码)

  • x + ~x = -1
  • x - x = 0
  • 得-x = ~x + 1

6. isAsciiDigit 函数

若 x 为 ASCII 的数字返回 1,否则 0

思路 1:

  • 判定x - 0x30 >=0
  • 判定0x39 - x >=0
  • 减 x 用到前一题的~x+1
1
2
3
4
5
6
7
8
9
int isAsciiDigit(int x) {
  int lower_bound = x + (~0x30 + 1);
  int upper_bound = 0x39 + (~x + 1);

  int lower_ok = !(lower_bound >> 31);
  int upper_ok = !(upper_bound >> 31);

  return lower_ok & upper_ok;
}

思路 2:

检查 x 如下图

1
2
|24bit |4bit|4bit |
|00..00|0011|0 ~ 9|

代码实现

1
2
3
4
5
6
7
8
9
10
int isAsciiDigit(int x) {
  int all_zero = !(x >> 8);
  int upper_nibble = !(((x >> 4) & 0xf) ^ 0x3);
  int lower_nibble = x & 0xf;
  // 9 - x >= 0
  int less_nine = 9 + (~lower_nibble + 1);
  int less_nine_ok = !(less_nine >> 31);

  return less_nine_ok & all_zero & upper_nibble;
}
  • 笔记: 检测 x 是否为负数等价于检查符号位是 0/1

7. conditional 函数

实现仿三目运算符

一开始的错误思路:

1
2
3
4
5
6
7
8
9
10
int conditional(int x, int y, int z) {
  // 掩码计算有误
  int y_mask = ~(!x);  // 0xff..ff
  int z_mask = ~x;  // 0xff..ff

  int left = (y_mask & y);
  int right = (z_mask & z);
  // 这里 left&1得不到left
  return (left & (!!x)) | (right & (!x));
}

改正后(思路见注释):

1
2
3
4
5
6
7
8
int conditional(int x, int y, int z) {
  int x_ok = !!x;
  // 当x!=0 y_mask应该=0xff..ff(实际是-1的补码)
  int y_mask = ~x_ok + 1;
  // 当x!=0 z_mask应该=0x00..00
  int z_mask = ~y_mask;
  return (y & y_mask) | (z & z_mask);
}

8. isLessOrEqual 函数

x<=y 就返回 1,否则 0

思路:

  • y - x >= 0检查该不等式即可

9. logicalNeg 函数

实现!运算符

思路:

  • 0 的特征=>0x00..00全 0
  • ±0 都是本身
  • x | (-x)判定符号位是否为 1,转换为式子结果是-1(非 0 时)
1
2
int logicalNeg(int x) { return (((x | (~x + 1)) >> 31) & 1) ^ 1; }
int logicalNeg(int x) { return ((x | (~x + 1)) >> 31) + 1; } // 进一步小优化

10. howManyBits 函数

返回最少用多少位表示 x

思路:

  • 正数:

    • 最高有效位 1 的位置加 1(符号位)

  • 负数

    • 最高有效位 0 的位置加 1

再翻译一下:

  • 先把一个 x 先变为 ~x(x<0 时)
  • 再将这个正数写成 32 位的二进制,需要找到最高有效位 1 的位置(书的课后作业 2.66 类似)
    • 位填充/位传播
      • 后续问题,怎么统计多少个 1(0x00..111 这样的数)popcount
    • 二分查找

我的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
int howManyBits(int x) {
  // 算数右移(容易单纯想成取符号位)
  int sign = x >> 31;
  // x = ~x(x<0) sign = 0xff..ff
  // x = x(x>0) sign = 0x00..00
  x = (sign & ~x) | (~sign & x);
  int is_zero = !x;

  // 位填充
  x |= x >> 1;
  x |= x >> 2;
  x |= x >> 4;
  x |= x >> 8;
  x |= x >> 16;

  // popcount
  int mask = 0x55;
  mask = mask | (mask << 8);
  mask = mask | (mask << 16);
  x = (x & mask) + ((x >> 1) & mask);  // 每2位1的个数

  mask = 0x33;
  mask = mask | (mask << 8);
  mask = mask | (mask << 16);
  x = (x & mask) + ((x >> 2) & mask);  // 每4位1的个数

  mask = 0x0f;
  mask = mask | (mask << 8);
  mask = mask | (mask << 16);
  x = (x & mask) + ((x >> 4) & mask);  // 每8位1的个数

  int mask_zero = 0x00;
  mask_zero = mask_zero | (mask_zero << 8);
  mask = 0xff;
  mask = mask | mask_zero;
  mask = mask | (mask << 16);
  x = (x & mask) + ((x >> 8) & mask);  // 每16位1的个数

  mask_zero = mask_zero | (mask_zero << 16);
  mask = 0xff;
  mask = mask | (mask << 8);
  mask = mask | mask_zero;

  x = (x & mask) + ((x >> 16) & mask);  // 32位1的个数

  int res = x + 1;

  return (res & ~is_zero) | (is_zero & 1);
}

claude 提供(二分)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int howManyBits(int x) {
    int sign = x >> 31;
    // 如果是负数，按位取反；如果是正数，保持不变
    x = (sign & ~x) | (~sign & x);

    // 检查是否为零
    int is_zero = !x;

    // 找到最高位的1，通过位填充
    int bit16, bit8, bit4, bit2, bit1, bit0;

    // 检查高16位是否有1
    bit16 = !!(x >> 16) << 4;
    // 4 -> 2^4
    // 如果有1，在高位找1的具体位置(二分体现)；否则保持原样
    x = x >> bit16;

    // 检查高8位是否有1
    bit8 = !!(x >> 8) << 3;
    x = x >> bit8;

    // 检查高4位是否有1
    bit4 = !!(x >> 4) << 2;
    x = x >> bit4;

    // 检查高2位是否有1
    bit2 = !!(x >> 2) << 1;
    x = x >> bit2;

    // 检查次高位是否有1
    bit1 = !!(x >> 1);
    x = x >> bit1;

    // 检查最低位是否有1
    bit0 = x;

    // 计算结果：所有bit的和加1（符号位）
    int bits = bit16 + bit8 + bit4 + bit2 + bit1 + bit0 + 1;

    // 处理零的特殊情况：零只需要1位
    return (bits & ~is_zero) | (is_zero & 1);
}

笔记:

  1. x = (sign & ~x) | (~sign & x)保留正 x,负 x 变~x
  2. !!(x >> 16)判定高 n 位有没有 1
  3. 位填充
  4. popcount

11. floatScale2 函数

返回 2*f

思路:

求出 s , exp, frac

  • 分 3 类讨论
    • 规格化
      • exp++再拼起来, 如果exp==255返回 ∞
    • 非规格化
      • frac<<1再拼起来
    • 特殊值
      • 返回 f

个人理解:

  • 规格化的情况(1.frac)
    • f*2,主要是整数部分*2
    • exp=>影响的是 E(exp-bias) => 2^E(exp++,E++,对应就是*2 了)
  • 非规格化的情况(0.frac)
    • f*2,主要是小数部分*2
    • frac=>影响的是 M(frac)=>(frac<<1,就相当于*2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
unsigned floatScale2(unsigned uf) {
  unsigned exp = (uf >> 23) & 0xff;
  unsigned frac = uf & 0x7fffff;
  unsigned s = (uf >> 31) & 0x1;
  // ∞和NaN
  if (exp == 0xff) {
    return uf;
  }
  // 非规格化
  else if (!exp) {
    return (s << 31) | (exp << 23) | (frac << 1);
  }
  // 规格化
  else {
    exp++;
    if (exp == 0xff) {
      return (s << 31) | (exp << 23);
    }
    return (s << 31) | (exp << 23) | frac;
  }
}

12. floatFloat2Int 函数

返回(int)f

思路:

  • 分 3 类讨论
    • 规格化
      • E<0 => 0(太小)
      • E>=31 => 0x80000000u(爆 int)
      • 正常转
    • 非规格化
      • 太小,返回 0
    • 特殊值
      • 返回 0x80000000u

按图示的逆过程:

int转float

一开始的写法:

1
2
3
4
5
6
7
8
9
10
11
12
13
E = exp - bias;
if (E < 0) {
  return 0;
} else if (E >= 31) {
  return 0x80000000u;
} else {
  // 这里有个漏洞,当 E>23, 未定义行为
  // 为什么我这个能过, E>23, right始终为0
  int point_right = frac >> (23 - E) & 0xffffff;
  int point_left = 1 << E;
  int merge = point_right | point_left;
  return s ? -merge : merge;
}

修正后:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
int floatFloat2Int(unsigned uf) {
  int E;
  unsigned exp = (uf >> 23) & 0xff;
  unsigned frac = uf & 0x7fffff;
  unsigned s = (uf >> 31) & 0x1;
  unsigned bias = 127;
  if (exp == 0xff) {
    return 0x80000000u;
  } else if (!exp) {
    return 0;
  } else {
    E = exp - bias;
    // 太小了
    if (E < 0) {
      return 0;
    }
    // 爆int
    else if (E >= 31) {
      return 0x80000000u;
    } else {
      // 拼起来
      int M = (1 << 23) | frac;
      if (E <= 23) {
        // 去除0
        M >>= (23 - E);
      } else {
        // 补0
        M <<= (E - 23);
      }
      return s ? -M : M;
    }
  }
}

13. floatPower2 函数

返回 2.0^x

思路:

  • 先在稿纸写一下 2.0 的表示和 4.0 的表示,发现 exp 部分(从 2=>4)+1 即可
  • 规格数: exp 范围在 1-254,找出范围(x >= -126 && x <= 127)
  • 非规格数: frac 里每个位都可以是 1

说实话一开始也不知道(x >= -149 && x < -126)这个范围怎么处理

这个范围还是用./btest -f floatPower2 -149测试脚本测出来的 😂

1
2
3
4
5
6
7
8
9
10
11
12
unsigned floatPower2(int x) {
  if (x > 127) {
    return 0x7f800000;
  } else if (x >= -126 && x <= 127) {
    unsigned exp = 127 + x;
    return exp << 23;
  } else if (x >= -149 && x < -126) {
    return 1 << (x + 149);
  } else {
    return 0x0;
  }
}

注意事项

dlc 检查

1
./dlc bits.c # 检查时,你的变量要定义在函数开头,否则会报错的

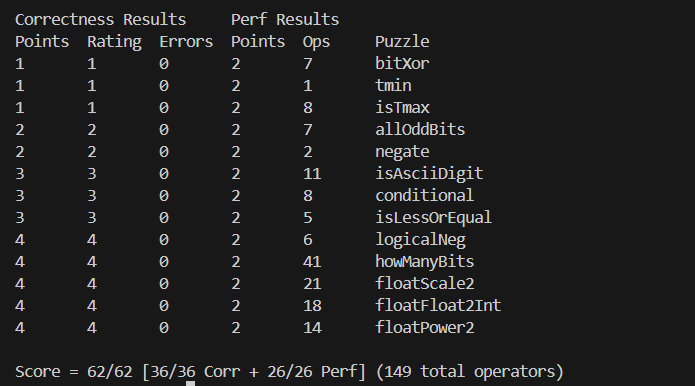
成果

dlc

btest

driver

总结

做 csapp 的 lab 真的很有意思，做出来跑测试脚本看到分数上涨，成就感满满 🥰🥰。个人觉得最难的应该是 howManyBits 这个题。整个 lab 零零散散花了 3 天才做完，菜菜的，不过确确实实学到东西了，接着加油。