2025.1.10 重启算法之旅

摩尔投票

题目:169. 多数元素

思路:摩尔投票法，每次遇到相同的数就加一，遇到不同的数就减一，最后剩下的数就是众数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int majorityElement(vector<int>& nums) {
    int candidate = 0, vote = 0;
    for (int n : nums) {
        if (vote == 0) {
            candidate = n;
        }
        if (n == candidate) {
            vote++;
        } else {
            vote--;
        }
    }
    return candidate;
}

荷兰国旗问题

题目:75. 颜色分类

思路:荷兰国旗问题，将数组切两刀，分左右，中间不用动。

特点:专门为这种有三种值的排序优化

image

参考，漫画:常考的荷兰国旗问题你还不会吗？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void sortColors(vector<int>& nums) {
    int begin = 0, end = nums.size() - 1, cur = 0;
    while (cur <= end) {
        if (nums[cur] == 0) {
            swap(nums[begin], nums[cur]);
            cur++;
            begin++;
        } else if (nums[cur] == 1) {
            cur++;
        } else {
            swap(nums[end], nums[cur]);
            end--;
        }
    }
}

龟兔赛跑

题目:142. 环形链表 II

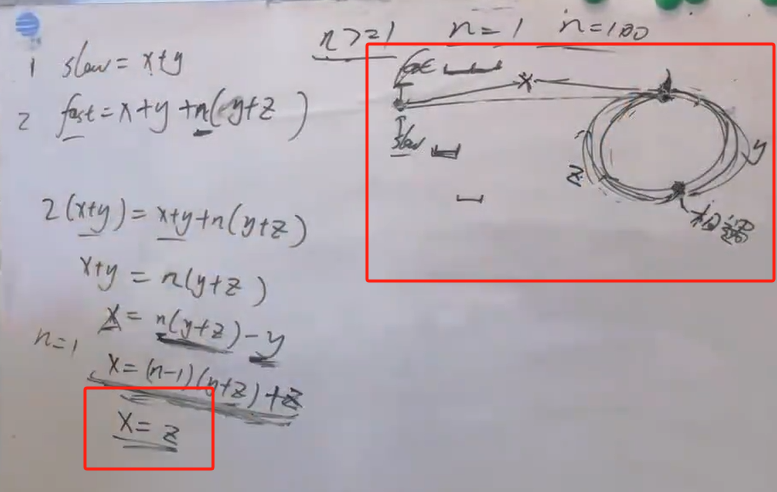
思路:龟兔赛跑，龟一次走一步，兔一次走两步，如果有环，龟兔一定会相遇，然后龟从头开始，兔从相遇点开始，每次都走一步，相遇的点就是环的入口。

image

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
while (true) {
    slow = nums[slow];
    fast = nums[nums[fast]];
    if (fast == slow) {
        break;
    }
}
// 相遇证明有环

slow = 0;
while (true) {
    slow = nums[slow];
    fast = nums[fast];
    if (slow == fast) {
        break;
    }
}
// 再次相遇就是环的入口

题目:287. 寻找重复数

只有两次重复的话,直接用等差数列求和减去数组和就是重复的数

思考一些变式

取二进制每位的操作

1
int bit = num >> i & 1; // 取第i位的二进制 10_000_000

统计每位 1 的个数

1
2
3
4
5
6
7
vector<int> bit_cnt(32, 0);
int num = 10;
for(int k =0;k<32;k++){
    if(num&(1<<k)) {
        bit_cnt[k]++;
    }
}

Pow(x, n)

题目:50. Pow(x, n)

思路: 快速幂,x^n = x^(n/2)*x^(n/2)

二进制为 1 计算结果,0 叠加权值

1
2
3
4
5
6
7
while (N > 0) {
    if (N & 1) {
        ans *= x;
    }
    x *= x;
    N >>= 1;
}

更好写和理解的一版

1
2
3
4
5
6
7
8
9
while (N > 0) {
    if (N % 2 == 1) {
        ans = ans * x;
    }
    // 平方
    x *= x;
    // 指数减半
    N /= 2;
}

并查集

1
2
3
4
5
6
7
// 初始化
int fa[N];
void init(int n) {
    for(int i = 0; i < n; i++) {
        fa[i] = i;
    }
}
1
2
3
4
// 查询
int find(int x) {
    return fa[x] == x ? x : find(fa[x]);
}
1
2
3
4
// 合并
void merge(int x, int y) {
    fa[find(x)] = find(y);
}
1
2
3
4
// 路径压缩
int find(int x) {
    return fa[x] == x ? x : (fa[x] = find(fa[x]));
}

除法求值

题目:399. 除法求值

思路: 带权并查集

公式

weight[x] 存储了从 x 到其父节点 fa[x] 的比例值

merge 函数

1
2
3
4
5
6
7
8
void merge(int from, int to, double val) {
  auto x = find(from);
  auto y = find(to);
  if (x != y) {
    fa[x] = y;
    weight[x] = val * weight[to] / weight[from];
  }
}

merge 更新权值公式推导(五个公式合并求解)

得

堆排序

定义一个 priority_queue

定义一个 priority_queue，默认情况下它使用 vector 作为底层容器，并使用 less 作为比较函数，这意味着最大的元素会被放在队列的顶部。

1
priority_queue<int> pq; // 用于 int 类型，默认大根堆

使用小根堆，定义如下:

1
priority_queue<int, vector<int>, greater<int>()> pq; // 小根堆

建堆:

1
2
std::make_heap(num.begin(), num.end());// 大根堆
std::make_heap(num.begin(), num.end(), std::greater<int>());// 小根堆

插入元素

使用 push() 方法来插入元素到 priority_queue 中。

1
2
3
pq.push(10);
pq.push(30);
pq.push(20);

访问顶部元素

使用 top() 方法来访问 priority_queue 的顶部元素，该元素是具有最高优先级的元素。

1
int topElement = pq.top(); // topElement 现在是 30

删除顶部元素

使用 pop() 方法来移除 priority_queue 的顶部元素。

1
pq.pop(); // 删除顶部元素，即 30

差分(区间更新)

基本概念

  1. 原始数组：nums = [a0, a1, a2, ..., an-1]
  2. 差分数组：diff，其中 diff[i] = nums[i] - nums[i-1]（假设 nums[-1] = 0）

区间更新操作

对区间 [l, r] 的所有元素加 k 时：

  • 只需在 diff[l] += k（表示从 l 开始都增加了 k）
  • 在 diff[r+1] -= k（表示从 r+1 开始取消这个增加）

还原原始数组

计算差分数组的前缀和，可以得到每个位置的实际值

1
2
3
nums[0] = diff[0]
nums[1] - nums[0] = diff[1]
nums[2] - nums[1] = diff[2]

零数组变换 I

题目:3355. 零数组变换 I

子数组(一般和前缀和有关)

和为 k 的子数组

题目:560. 和为 K 的子数组

思路:前缀和+哈希表

暴力写法:
思考: 暴力写法，时间复杂度是 O(n^2)
下面这个部分可能可以优化(全部正数提前跳出)

1
2
3
4
cur += nums[j];
if (cur == k) {
    ans++;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
int subarraySum(vector<int>& nums, int k) {
    int ans = 0;
    for (int i = 0; i < nums.size(); i++) {
        int cur = 0;
        for (int j = i; j < nums.size(); j++) {
            cur += nums[j];
            if (cur == k) {
                ans++;
            }
        }
    }
    return ans;
}

用哈希表来优化，将前缀和存入哈希表中，然后每次遍历的时候，判断当前前缀和减去 k 是否在哈希表中，如果在，说明存在一个子数组，其和为 k。
为什么可以前缀和? s[j]−s[i]=k (i<j)前缀和数组的差是子数组的和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int subarraySum(vector<int>& nums, int k) {
    int ans = 0;
    unordered_map<int, int> pre_sum_cnt;
    pre_sum_cnt[0] = 1;
    int pre_sum = 0;
    for (int& num : nums) {
        pre_sum += num;
        if (pre_sum_cnt.find(pre_sum - k) != pre_sum_cnt.end()) {
            ans += pre_sum_cnt[pre_sum - k];
        }
        pre_sum_cnt[pre_sum]++;
    }
    return ans;
}

路径总和 III(做法同上)

题目:437. 路径总和 III

1
2
3
4
5
6
7
8
9
10
11
12
13
int dfs(TreeNode* root, long long curSum, int targetSum,
        unordered_map<long long, int>& cnt) {
    if (!root)
        return 0;

    curSum += root->val;
    int ans = cnt[curSum - targetSum];
    cnt[curSum]++;
    ans += dfs(root->left, curSum, targetSum, cnt);
    ans += dfs(root->right, curSum, targetSum, cnt);
    cnt[curSum]--;
    return ans;
}

轮转数组

题目:189. 轮转数组

思路:三次翻转

1
2
3
4
5
void rotate(vector<int>& nums, int k) {
    int n = nums.size();
    k = k % n;
    std::rotate(nums.begin(), nums.begin() + (n - k), nums.end()); // stl自带的轮转函数,底层还是三次翻转,时间复杂度是O(n)
}

或值至少 K 的最短子数组

小结论:

  1. | 或运算的结果要么不变，要么变大。
  2. & 与运算的结果要么不变，要么变小。

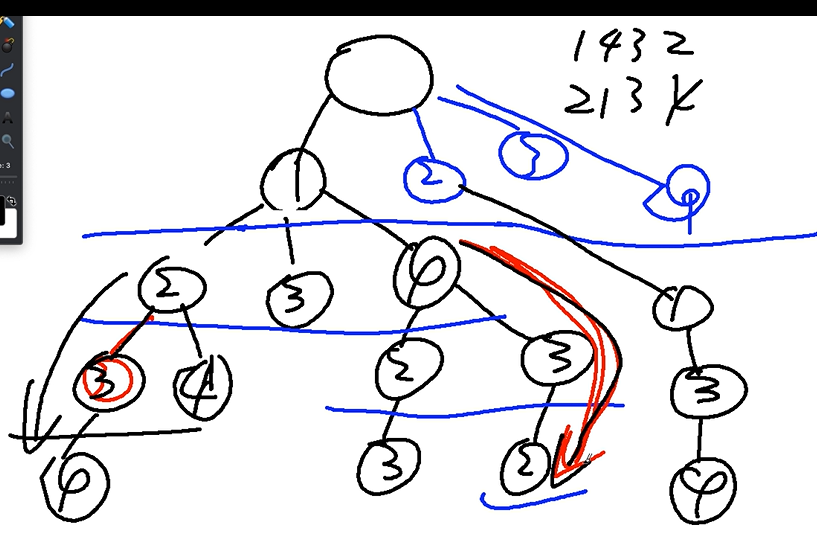
下一个排列

画 dfs 图好理解，找规律

思路: 从后往前找，找到第一个 nums[i] < nums[i+1] 的位置(左往右看升序)，然后从后往前找第一个 nums[j] > nums[i] 的位置，交换 nums[i] 和 nums[j]，然后将 i 之后的元素翻转。

1
2
#include <algorithm>
std::next_permutation(nums.begin(), nums.end());// stl自带的下一个排列函数

栈类型题

处理 string，有括号，可以想到用栈

1
isdigit(ch) // 判断字符是否是数字

下一个更大的元素，这类型的问题通常可以用单调栈来解决

单调栈

单调递增栈: 元素从栈底到栈顶是递增的（栈顶元素最大）找到“最近更小值”
单调递减栈: 元素从栈底到栈顶是递减的（栈顶元素最小）找到“最近更大值”

1
2
3
4
5
6
7
8
9
stack<int> st;
for (int i = 0; i < n; i++) {
    while (!st.empty() && temperatures[i] > temperatures[st.top()]) {
        int top_idx = st.top();
        ans[top_idx] = i - top_idx;
        st.pop();
    }
    st.push(i);
}

柱状图中最大的矩形

题目:84. 柱状图中最大的矩形

暴力思路: 找到左右边界(比当前小的)，然后计算面积

暴力写法:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
for (int i = 0; i < n; i++) {
    int left = i, right = i;

    while (left > 0 && heights[left - 1] >= heights[i]) {
        left--;
    }

    while (right < n - 1 && heights[right + 1] >= heights[i]) {
        right++;
    }

    int width = right - left + 1;
    int area = heights[i] * width;
    max_area = max(max_area, area);
}

优化策略: 单调递增栈，找到左右边界(比当前小的)

单调队列

滑动窗口最大值

题目:239. 滑动窗口最大值

思路: 单调递减队列，队列中存储的是下标，队列中元素的下标是单调递增的，队列中元素的值是单调递减的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
for (int i = 0; i < n; i++) {
    // 入
    while (!q.empty() && nums[q.back()] <= nums[i]) {
        q.pop_back();
    }
    q.push_back(i);
    // 出
    if (i - q.front() >= k) {
        q.pop_front();
    }
    // 更新ans
    if (i >= k - 1) {
        ans.push_back(nums[q.front()]);
    }
}

二分查找

找中间点

1
2
// 注意这里防止 (left+right) 溢出
int mid = left + (right - left) / 2;

ai 总结

  1. 核心思想:
    关键在于如何缩小搜索范围。每次迭代后，确保搜索空间中仍然包含目标值。
  2. 选择合适的终止条件
    1. 如果需要找到唯一解，使用 while (left < right)
    2. 如果需要检查所有可能的解，使用 while (left <= right)
  3. 理解更新规则
    1. 如果 nums[mid] 可能是解，不要跳过它（如 right = mid）
    2. 如果确定 nums[mid] 不是解，可以直接排除（如 left = mid + 1 或 right = mid - 1）

搜索旋转排序数组

题目:33. 搜索旋转排序数组

结论: 将区间分均分，必然有一半有序，一半无序。

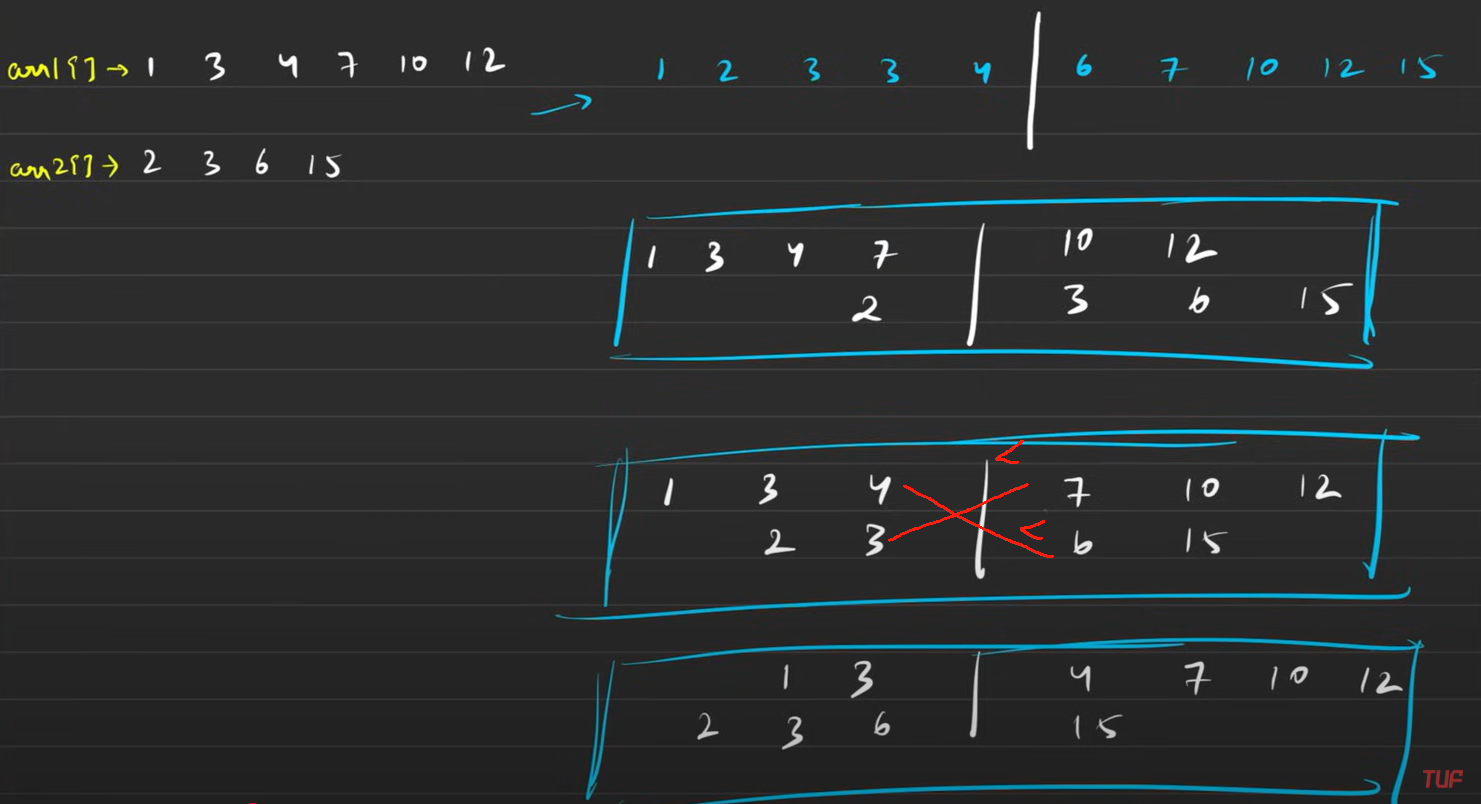
寻找两个正序数组的中位数

题目:4. 寻找两个正序数组的中位数

思路:

  1. 二分查找
  2. findKth

边界条件:
num1 的左边最大值 <= num2 的右边最小值
num1 的右边最小值 >= num2 的左边最大值

边界

袋子里最少数目的球

题目:1760. 袋子里最少数目的球

思路: 二分答案 + check

关键函数

1
2
3
4
5
6
7
8
9
10
11
12
13
// 在 maxOperations 次操作内，能否将所有球分割成<= maxSize 的若干份
bool check(const vector<int>& nums, int maxOperations, int maxSize) {
    int op = 0;
    for (int num : nums) {
        if (num > maxSize) {
            op += (num - 1) / maxSize;
        }
        if (op > maxOperations) {
            return false;
        }
    }
    return true;
}

两球之间的磁力

题目:1552. 两球之间的磁力

思路: 二分答案 + check

关键函数

1
2
3
4
5
6
7
8
9
10
11
// 最小能放x分
bool check(int x, vector<int>& position, int m) {
    int pre = position[0], cnt = 1;
    for (int i = 1; i < position.size(); ++i) {
        if (position[i] - pre >= x) {
            pre = position[i];
            cnt += 1;
        }
    }
    return cnt >= m;
}

在排序数组中查找元素的第一个和最后一个位置

题目:34. 在排序数组中查找元素的第一个和最后一个位置

思路: 二分查找，先找左边界，(如果找到)，再更新 left 指针，找右边界

库函数: (有序数组二分查找)

1
2
3
4
5
6
7
8
9
lower_bound(nums.begin(), nums.end(), target);
upper_bound(nums.begin(), nums.end(), target);
// map 和 set直接提供了 upper_bound 成员函数
map<int, int> m;
m.upper_bound(key);
m.lower_bound(key);
set<int> s;
s.upper_bound(key);
s.lower_bound(key);

每一个查询的最大美丽值

题目:2070. 每一个查询的最大美丽值

思路：对 items 排序, 用 map 记录每个位置的最大值, 然后用二分查找(upper_bound)找到第一个大于等于 query 的位置, 更新答案

旋转图像

题目:48. 旋转图像

思路: 矩阵转置，反转每一行

额外数组: 索引关系 tmp[j][n - 1 - i] = matrix[i][j]

记忆方法

螺旋矩阵

题目:54. 螺旋矩阵

思路: 模拟，每次走完一条边，就改变方向

1
2
3
4
5
6
7
8
9
10
11
12
13
while (true) {
    for (int i = left; i <= right; i++) ans.push_back(matrix[up][i]);
    if (++up > down) break;

    for (int i = up; i <= down; i++) ans.push_back(matrix[i][right]);
    if (--right < left) break;

    for (int i = right; i >= left; i--) ans.push_back(matrix[down][i]);
    if (--down < up) break;

    for (int i = down; i >= up; i--) ans.push_back(matrix[i][left]);
    if (++left > right) break;
}

螺旋矩阵 | 手写图解版思路

排序链表

题目:148. 排序链表

思路: 快慢指针找到中点，断链表，对左右链表排序，然后合并两个有序链表

子集

题目:78. 子集

思路: dfs，不选当前 nums[i]元素，或者选他，然后要弹出(恢复现场)，递归 dfs(i+1)后面的元素。

子集 II

题目:90. 子集 II

思路:

  1. 和子集那题一样，但是需要先对数组排序，这样相同的元素就会挨在一起，最后用 set 去重。
  2. 在 dfs 的时候，选当前 nums[i]元素，然后要弹出(恢复现场)，i++往后走，他如果当前元素和前一个元素相同，那么就跳过，递归 dfs(i)后面的元素。

验证回文串

题目:125. 验证回文串

思路: 先处理字符串，再双指针，从两边往中间走，判断是否相等。

处理字符串:

  1. 将字符串转为小写tolower(char c)
  2. 判断字符是否是字母或数字isalnum(char c)
1
2
3
4
5
for (char c : s) {
    if (isalnum(c)) {
        processed += tolower(c);
    }
}

最长回文子串

题目:5. 最长回文子串

暴力思路: O(n^2)找每个子串，再双指针 check 子串是不是回文串

dp 思路: dp[i][j]代表[i..j]是否回文

  1. 先初始化长度为 1 和 2 的
  2. 再从长度为 3 去拓展(s[i] == s[j] && dp[i + 1][j - 1])

中心拓展:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int expand(string& s, int left, int right) {
    while (left >= 0 && right < s.size() && s[left] == s[right]) {
        left--;
        right++;
    }
    // 循环结束是多走了一格(right-1)-(left+1)+1
    return right - left - 1;
}

for (int i = 0; i < s.size(); i++) {
    int oddLen = expand(s, i, i);
    int evenLen = expand(s, i, i + 1);
    // 奇偶拓展拿最大再更新
    int len = max(oddLen, evenLen);
    if (len > maxLength) {
        maxLength = len;
        start = i - (len - 1) / 2;
    }
}

不同路径 II

题目:63. 不同路径 II

暴力思路: 分别尝试向下和向右走，类似二叉树 O(2^(m+n))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void dfs(int x, int y, int m, int n, vector<vector<int>>& grid) {
    if (x == m-1 && y == n-1) {
        ans++;
        return;
    }

    // 向右
    if (y + 1 < n && grid[x][y+1] == 0) {
        dfs(x, y+1, m, n, grid);
    }
    // 向下
    if (x + 1 < m && grid[x+1][y] == 0) {
        dfs(x+1, y, m, n, grid);
    }
}

优化: 加上记忆化搜索，memo 数组存储已计算过的数 O(m*n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int dfs(int x, int y, int m, int n, vector<vector<int>>& grid) {
    // 如果已经计算过这个位置，直接返回记录的值
    if (memo[x][y] != -1) {
        return memo[x][y];
    }

    if (x == m - 1 && y == n - 1) {
        return 1;
    }

    int paths = 0; // 记录从当前位置到终点的路径数

    // 向右
    if (y + 1 < n && grid[x][y + 1] == 0) {
        paths += dfs(x, y + 1, m, n, grid);
    }
    // 向下
    if (x + 1 < m && grid[x + 1][y] == 0) {
        paths += dfs(x + 1, y, m, n, grid);
    }

    // 记录当前位置的结果
    memo[x][y] = paths;
    return paths;
}

dp 思路: dp[i][j] = dp[i-1][j] + dp[i][j-1]，到达当前格子的路径数等于从上面来的路径数加上从左边来的路径数 O(m*n)

单词搜索

题目:79. 单词搜索

思路: dfs，每次尝试向四个方向走，用二维 bool 数组 visited 记录走过的路径(回溯操作就很方便了)，如果走不通，就回溯，恢复现场。

回溯

1
2
3
visited[i][j] = true;
dfs();
visited[i][j] = false;

优化策略:

  1. 先看看 board 里面有没有足够的字母拼凑出 wordunordered_map<char, int> board_cnt，如果不够，直接返回 false
  2. 比较 word 的首尾字母在 board 里的个数cnt[word.back()] < cnt[word[0]]，优先从少的字母开始搜索(reverse(word.begin(), word.end()))

01 背包

一个数组的写法 dp 要逆序计算

完全背包

灵神 tips: 外层循环枚举物品，内层循环枚举体积(完全背包)

一个数组的写法 dp 可以正序计算

从 dfs 边界反推 dp 数组

零钱兑换

题目:322. 零钱兑换

思路: dfs，每次尝试拿 1-amount 的钱，然后递归 dfs(amount - coin)，如果 amount == 0，说明找到了一种方案，返回 0，否则返回 -1。

完全平方数

题目:279. 完全平方数

思路: dfs，每次尝试拿 1-n 的数，然后递归 dfs(n - i*i)，如果 n == 0，说明找到了一种方案，返回 0，否则返回 -1。

统计相似字符串对的数目

题目:2506. 统计相似字符串对的数目

思路: 哈希表加位运算(状态压缩)

1
2
3
for (char c : w) {
    mask |= 1 << (c - 'a'); // 将字母映射到二进制位, 1出现, 0未出现
}

滑动窗口

两种更新 ans 的方式

更新方式 用法场景 示例题目
ans += right - left + 1 统计以当前 right 结尾的所有合法子数组个数 2302. 统计得分小于 K 的子数组数目
ans += n - right 统计以当前 left 开头的所有合法子数组个数 2962. 统计最大元素出现至少 K 次的子数组

找到字符串中所有字母异位词

题目:438. 找到字符串中所有字母异位词

思路: 滑动窗口，用两个数组记录 s 和 p 中每个字母出现的次数，然后比较两个数组是否相等。

大致模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int left = 0, right = 0; // 窗口的左右指针
int windowSize = p.size(); // 窗口大小

while (right < s.size()) {
    // 扩展窗口：右指针右移，更新窗口状态
    windowCount[s[right] - 'a']++;
    right++;

    // 当窗口大小达到目标大小时，开始收缩窗口
    if (right - left == windowSize) {
        // 检查当前窗口是否满足条件
        if (windowCount == pCount) {
            result.push_back(left); // 满足条件，记录结果
        }

        // 收缩窗口：左指针右移，更新窗口状态
        windowCount[s[left] - 'a']--;
        left++;
    }
}

字符串滑窗用s.substr(left, right - left)获取窗口结果

设计一个文本编辑器

题目:2023. 设计文本编辑器

思路: 双栈，一个栈记录光标左边的字符，一个栈记录光标右边的字符。

犯错点:

1
2
3
text.substr(pos); // 直接从 pos..到结尾
text.substr(pos, len); // 第二个参数是长度
text.erase(pos); // 直接删除 pos..到结尾

最长公共子序列

题目:1143. 最长公共子序列

递归思路:

如果 text1[i] == text2[j]，那么这个字符可以作为公共子序列的一部分，接着递归比较 text1[i+1:] 和 text2[j+1:]。
如果 text1[i] != text2[j]，则有两种选择：
跳过 text1[i]，递归比较 text1[i+1:] 和 text2[j:]。
跳过 text2[j]，递归比较 text1[i:] 和 text2[j+1:]。

边界条件:

如果 i == len(text1) 或 j == len(text2)，说明一个字符串已经遍历完，此时公共子序列长度为 0。

课程表

题目:207. 课程表

思路: 拓扑排序 kahn

  1. 统计每个节点的入度
  2. 将入度为 0 的节点加入队列，维护一个 cnt(已访问的节点数)
  3. 每次从队列中取出一个节点，将它指向的节点的入度减 1，如果入度为 0，将它加入队列
  4. 重复 3，直到队列为空
  5. 如果 cnt == numCourses，说明所有节点都被访问过，返回 true，否则返回 false

思路: dfs

  1. 用二维数组记录每个节点的出边(邻接表)
  2. 用一维数组记录每个节点的状态，0 表示未访问，1 表示递归栈里已访问(跳过)，2 表示已访问(有环)
  3. 从每个节点开始 dfs，如果发现有环，返回 false
  4. 如果所有节点都没有环，返回 true

b 站讲解视频

二叉树

bfs 模板

  1. 单节点操作
1
2
3
4
5
6
7
8
9
10
11
12
queue<TreeNode*> q;
q.push(root);

while (!q.empty()) {
    TreeNode* node = q.front();
    q.pop();

    // 操作

    if (node->left != nullptr) q.push(node->left);
    if (node->right != nullptr) q.push(node->right);
}
  1. 分层操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
queue<TreeNode*> q;
q.push(root);

while (!q.empty()) {
    int levelSize = q.size();
    vector<int> currentLevel;

    for (int i = 0; i < levelSize; ++i) {
        TreeNode* node = q.front();
        q.pop();

        // 当前节点操作
        currentLevel.push_back(node->val);

        if (node->left != nullptr) q.push(node->left);
        if (node->right != nullptr) q.push(node->right);
    }
    // 对该层的操作
}
  1. 双数组模拟队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
vector<TreeNode*> cur;
cur.push_back(root);

while (!cur.empty()) {
    int level_size = cur.size();
    vector<TreeNode*> nxt;

    for (int i = 0; i < level_size; i++) {
        auto node = cur[i];

        // 当前节点操作

        if (node->left) {
            nxt.push_back(node->left);
        }
        if (node->right) {
            nxt.push_back(node->right);
        }
    }
    cur = move(nxt);
}

数组美丽值求和

题目:2012. 数组美丽值求和

思路: 维护两个数组 left_max 和 right_min 来实现找左边最大,和右边最小,左边最大不能大于右边最小

对角线上的质数

题目:2614. 对角线上的质数

检查质数的思路:

  1. 从 2 开始，一直到 sqrt(n)，检查是否能整除
1
2
3
4
5
6
7
bool isPrime(int n) {
    if (n <= 1) return false;
    for (int i = 2; i * i <= n; i++) {
        if (n % i == 0) return false;
    }
    return true;
}
  1. 打表, 用一个 bool 数组(大小为 max_val+1)记录每个数是否是质数
1
2
3
4
5
6
7
8
9
10
vector<bool> isPrime(max_val + 1, true);
isPrime[0] = isPrime[1] = false;
for (int i = 2; i * i <= max_val; i++) {
    if (isPrime[i]) {
        // 将 i 的倍数标记为非质数
        for (int j = i * i; j <= max_val; j += i) {
            isPrime[j] = false;
        }
    }
}

最大或值

题目: 2680. 最大或值

将位 bit_cnt 数组转回数字

1
2
3
4
5
6
7
int ans = 0;
int bit_cnt[32];
for (int i = 0; i < 32; i++) {
    if (bit_cnt[i] > 0) {
        ans |= (1 << i);
    }
}

妙: 所有的 or 遍历到 x 用异或去掉 x 的影响

1
2
3
for (int x : nums) {
    ans = max(ans, (all_or ^ x) | fixed | ((long long) x << k));
}

判断一个括号字符串是否有效

题目: 2116. 判断一个括号字符串是否有效

思路:

  1. 两次遍历,前后各一次,都有效才有效

有效括号字符串通用模板:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool isValid(string s) {
    int balance = 0;
    for (char c : s) {
        if (c == '(') {
            balance++;
        } else {
            balance--;
            if (balance < 0) {
                return false;
            }
        }
    }
    return balance == 0;
}

最大正方形

题目: 221. 最大正方形

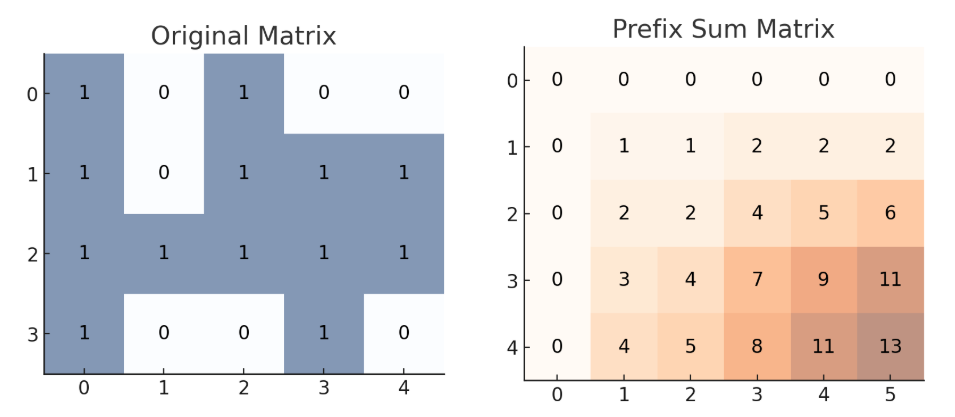
思路: 二维前缀和, 枚举边长, 查看是否全是 1

图示

原始矩阵的坐标(i,j)->前缀和矩阵的坐标(i+1,j+1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int maximalSquare(vector<vector<char>>& matrix) {
  auto m = matrix.size();
  auto n = matrix[0].size();
  // 构造前缀和
  auto pre = vector<vector<int>>(m + 1, vector<int>(n + 1, 0));
  for (int i = 1; i <= m; i++) {
    for (int j = 1; j <= n; j++) {
      pre[i][j] = pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1] +
                  (matrix[i - 1][j - 1] == '1');
    }
  }

  auto ans = 0;
  // 枚举size方便理解和编写代码, 从大到小枚举size, 找到第一个满足条件的size, 直接返回
  for (int size = min(m, n); size >= 1; size--) {
    if (size * size <= ans) {
      break;
    }
    for (int i = size; i <= m; i++) {
      for (int j = size; j <= n; j++) {
        auto sum = pre[i][j] - pre[i - size][j] - pre[i][j - size] +
                   pre[i - size][j - size];
        if (sum == size * size) {
          return sum;
        }
      }
    }
  }
  return ans;
}

找出字符串中第一个匹配项的下标

题目: 28. 找出字符串中第一个匹配项的下标

思路: kmp 模板题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
int strStr(string s, string p) {
  auto n = p.size();
  // 构造next数组
  auto next = vector<int>(n, 0);
  // pre_len相同前后缀长度
  for (int i = 1, pre_len = 0; i < n;) {
    if (p[i] == p[pre_len]) {
      next[i++] = ++pre_len;
    } else if (pre_len > 0) {
      pre_len = next[pre_len - 1];
    } else {
      next[i++] = 0;
    }
  }
  // kmp匹配
  auto i = 0;
  auto j = 0;
  while (i < s.size()) {
    if (s[i] == p[j]) {
      i++;
      j++;
    }
    // 失匹, 根据next跳过前面
    else if (j > 0) {
      j = next[j - 1];
    }
    // 一开始就不匹配, 直接跳过
    else {
      i++;
    }
    if (j == p.size()) {
      return i - j;
    }
  }
  return -1;
}

个人小结

指针走路类似一个追及问题

链表虚拟节点技巧

1
2
3
ListNode dummy(0, head);
ListNode *cur = &dummy;
return dummy.next;

std 库函数总结

  1. unique函数

std::unique 只能移除连续重复的元素,挪到后面,使用 std::unique 之前,需要先调用 std::sort 对数据进行排序

1
2
auto it = std::unique(nums.begin(), nums.end());  // 返回去重后的尾迭代器
nums.erase(it, nums.end());  // 搭配erase去除末尾的重复元素
  1. vector 实现头插
1
2
vector<int> v;
v.insert(v.begin(), 1);
  1. gcd函数

取最大公约数

1
int g = gcd(a, b); // 在头文件<numeric>中

底层实现

1
2
3
4
5
6
7
8
int gcd(int a, int b) {
    while (b != 0) {
        int temp = b;
        b = a % b;
        a = temp;
    }
    return a;
}
  1. lcm函数

取最小公倍数

1
int l = lcm(a, b); // 在头文件<numeric>中

底层实现

1
2
3
int lcm(int a, int b) {
    return a * b / gcd(a, b);
}

gcd 和 lcm 关联 LCM(a, b) × GCD(a, b) = a × b

  1. a/b向上取整公式
1
int res = (a - 1) / b + 1;
  1. getline(istream,string,char)函数

从输入流中读取一行字符串, 可以指定分隔符

1
2
3
4
5
6
string s = "hello/world/yes";
istringstream iss(s);
string tmp;
while (getline(iss, tmp, '/')) {
    cout << tmp << endl;
}
  1. 将单个数字加进 string
1
2
3
auto s = string{};
int n = 5;
s += static_cast<char>(n + '0');
  1. 不能当作哈希表键的类型
  • unordered_map
  • unordered_set
  1. find(first_iter, last_iter, target)函数
1
2
3
auto it = find(nums.begin(), nums.end(), 1);
// 取idx
int idx = it - nums.begin();